Le théorème de Pythagore : vous en souvenez-vous ? Pour tout savoir à son sujet

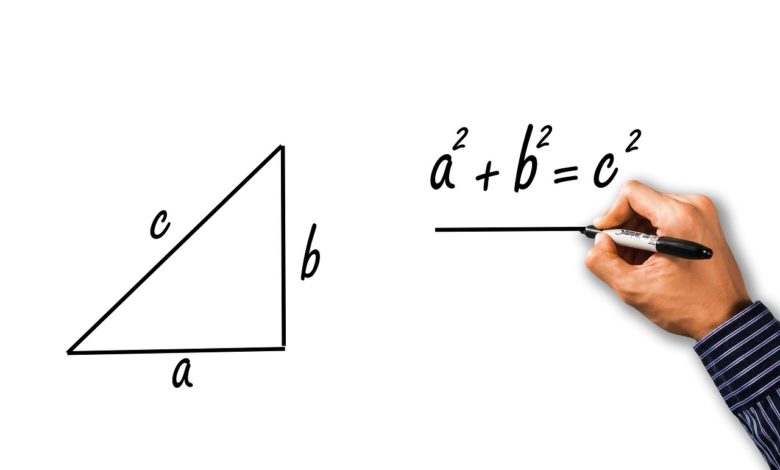
Un des premiers théorèmes de géométrie inculqués aux collégiens est celui de Pythagore. Une bête noire pour bon nombre d’élèves de 4ᵉ qui est en fait une loi mathématique toute simple. Les constructeurs en sont les premiers utilisateurs, mais ce n’est qu’une partie de son application. Tour d’horizon d’une formule plurimillénaire qui est omniprésente au quotidien, alors qu’il cache bien son jeu. Voici donc un retour sur son histoire qui n’a pas été détaillée à l’école. Focus également sur ses différentes applications et ses réelles implications.

Le théorème n’appartient pas à Pythagore

Contrairement aux idées reçues, ce n’est guère le scientifique et philosophe grec qui a inventé le fameux théorème qui porte son nom. Voilà une des premières informations à savoir sur le théorème de Pythagore. En effet, les Égyptiens auraient déjà eu des connaissances sur ce théorème 2 000 ans avant J.C.

Ceux-ci utilisaient notamment une corde à 13 nœuds équidistants pour obtenir des angles droits en formant un triangle via l’outil. Ce dernier servait encore aux maçons du 20ᵉ siècle afin de s’assurer de l’angle droit des murs.  Les Chinois et les Babyloniens étaient, eux aussi, au courant du théorème, 1 000 ans avant Pythagore, qui vécut entre 580 et 495 avant J.C.

Les fouilles archéologiques ont dévoilé des tablettes d’argile babyloniennes énonçant le théorème. Le rôle de Pythagore a été de l’améliorer afin de le rendre plus accessible à un plus large public. Concrètement, le théorème met en relation les longueurs des côtés d’un triangle rectangle. La longueur de l’hypoténuse au carré équivaut à la somme des carrés des longueurs des deux autres côtés.

Au fil des siècles, le théorème a pris diverses appellations. Les pythagoriciens de la Grèce antique l’appelèrent Théorème de la mariée. Les Hindous lui prêtèrent le nom de la Chaise de la mariée et durant le Moyen Âge, il a été nommé Maître de la mathématique. Sa réciproque, chez les Perses, a été appelée Chaise de la mariée. Ce n’est qu’au 20ᵉ siècle que le théorème porte finalement son nom.

Le savant est à l’origine de plusieurs travaux intellectuels d’envergure, que ce soit dans le domaine des mathématiques, de la philosophie ou de l’astronomie. Ayant vécu 85 ans, il passa son existence à œuvrer pour le bien de l’Humanité en avançant des théories novatrices pour son époque.

D’innombrables applications pour une simple formule

Considéré comme l’un des théorèmes les plus importants en mathématiques, le théorème de Pythagore revêt diverses applications. Il sert essentiellement à vérifier l’équerrage d’un ouvrage. Cependant, depuis l’Antiquité, il permet aussi de calculer les distances. Grâce à cette formule, il était possible de déterminer, entre autres, l’itinéraire le plus court pour rallier deux endroits.

Le théorème se révèle également très pratique pour déterminer des longueurs difficiles à mesurer. Les professionnels l’utilisent, en outre, pour obtenir la hauteur d’une montagne ou d’un bâtiment. De même, il est mis à profit pour calculer les dimensions de plusieurs constructions. Ce dernier entre ainsi dans le calcul du volume de certains objets ou récipients.

Les lycéens, quant à eux, découvrent qu’à part les mathématiques, le théorème est présent dans d’autres domaines. Les sciences physiques, la mécanique, l’électronique, l’informatique ou l’ingénierie sont autant de spécialités requérant la formule. Pour information, il est nécessaire pour calculer les forces qui s’exercent sur une structure donnée pour cela.

Dans la vie de tous les jours, les applications du théorème de Pythagore comprennent d’autres théorèmes plus élaborés. Sinon, il faut savoir que le théorème est à la base d’autres théories tout aussi célèbres. Cela est le cas de la série de Fourier et de la théorie des ondelettes.

Peu de gens soupçonnent encore qu’il est essentiel pour compresser les données JPEG. Il en est de même au temps des CD audio, dont le format dépendait du théorème. Face à l’engouement pour le théorème, plusieurs démonstrations ont été faites pour affirmer son énoncé.

Une loi trigonométrique qui a changé le cours de l’histoire

Au vu des nombreuses applications du théorème de Pythagore, sa découverte et sa formalisation par le savant grec ont été déterminantes quant à la configuration du monde actuel. À la base élaborée pour effectuer des mesures géométriques (trigonométrie), son apport a pourtant touché divers domaines.

Les constructions actuelles ne seraient pas ce qu’elles sont sans cette loi mathématique. Comment aurait fait l’architecte pour obtenir certaines mesures avec un simple plan sur papier ? Ou encore, quelle est l’assurance pour un maçon d’avoir des angles droits là où ils doivent l’être ? Voilà un petit aperçu des problématiques susceptibles de s’être posées sans ce célèbre théorème.

Connaissant l’importance de l’ingénierie envers les avancées techniques et technologiques, ceux qui ont douté de l’utilité de la formule c²=a²+b² peuvent maintenant revenir sur leurs dires. Le monde d’aujourd’hui ne serait tout simplement pas ce qu’il est sans le théorème de Pythagore.

Chacun connaît un des outils de prédilection des constructeurs, à savoir l’équerre. Cependant, tous oublient qui en est à l’origine. Les maisons ne sont pas de travers, grâce à celle-ci. Elle ne peut toutefois pas servir dans certains cas et c’est la formule qui doit être utilisée. De nos jours, des appareils plus sophistiqués ont remplacé l’équerre, mais se basant toujours sur la perpendicularité et son principe.

Pour le commun des mortels, il est impensable de cerner l’implication de ce théorème dans les diverses spécialités. Quasiment tout ce qui touche à l’humain, sur le plan physique, est lié à celui-ci. Voilà pourquoi le Théorème de Pythagore n’est pas une simple formule banale étudiée dans le cursus scolaire.

En résumé

Le soi-disant élève de Thalès a permis aux scientifiques qui lui ont succédé d’utiliser avec une grande simplicité le théorème relatif aux triangles rectangles. N’étant pas directement à l’origine du théorème qui porte son nom, il a participé à le rendre plus compréhensible. Généralement utilisé dans la construction, la loi sur la perpendicularité de ces types de triangles joue un rôle majeur dans plusieurs applications. De l’informatique, en passant par la mécanique et l’ingénierie, plusieurs branches d’activités s’en servent. L’humanité ne peut donc certainement pas continuer d’évoluer sans ce théorème. Qui sait s’il ne réserve pas d’autres bonnes surprises pour le futur ?